Сетевой график, пример построения

Основные определения

Ориентированный графназывается сетьюсетевой моделью или сетевым графикомработ и событий

• «действительная работа» – процесс, требующий затрат времени и ресурсов;
• «фиктивная работа» – логическая связь между двумя или несколькими работами, указывающая на то, что начало одной работы зависит от результатов другой. Фиктивная работа не требует затрат времени и ресурсов, продолжительность ее равна нулю.

начальноеiконечноеj

На сетевой модели событиям соответствуют вершины графа.

Правила построения сетевой модели

Правило 1

Правило 2. Ни одна пара операций не должна определяться одинаковыми начальным и конечным событиями. Возможность неоднозначного определения операций через события появляется в случае, когда две или большее число операций допустимо выполнять одновременно.

Правило 3. При включении каждой операции в сетевую модель для обеспечения правильного упорядочения необходимо дать ответы на следующие вопросы:
а) Какие операции необходимо завершить непосредственно перед началом рассматриваемой операции?
б) Какие операции должны непосредственно следовать после завершения данной операции?
в) Какие операции могут выполняться одновременно с рассматриваемой?

При построении сетевого графика следует соблюдать следующие правила:

• в сети не должно быть «тупиков», т.е., событий, от которых не начинается ни одна работа, исключая завершающее событие графика;
• В сетевом графике не должно быть «хвостовых» событий, то есть событий, которым не предшествует хотя бы одна работа, за исключением исходного.
• в сети не должно быть замкнутых контуров (рис.1);
• Любые два события должны быть непосредственно связаны не более чем одной работой.
• В сети рекомендуется иметь одно исходное и одно завершающее событие.
• Сетевой график должен быть упорядочен. То есть события и работы должны располагаться так, чтобы для любой работы предшествующее ей событие было расположено левее и имело меньший номер по сравнению с завершающим эту работу событием.

Пример построения сетевого графика

Несмотря на то, что описанный выше алгоритм может показаться сложным, на самом же деле построение сетевого графика задача несложная. Для того, чтобы убедиться в этом рассмотрим построение сетевого графика на простом примере ремонта детской комнаты.

Шаг 1. Определить основную цель проекта

Представьте, что сейчас лето, вашему сыну исполнилось 7 лет и в сентябре он идет в школу. Вы решил обновить его комнату к новому учебному году и сделать ее подходящей для школьника, т.е. должно появиться полноценной рабочее место, зонирование комнаты измениться, и т.д.

В этом случае целью нашего небольшого проекта будет —  сделать комнату пригодной и приятной для проживания мальчика, который пойдет в начальную школу.

Шаг 2. Выявить ограничения

Бюджет не более 100,000 руб., ремонтные работы можно вести только в рабочие дни с 10:00 до 18:00 с обязательным перерывом с 12:00 до 14:00. Итого получается — 6 рабочих часов в день.

Шаг 3. Определить состав работ

Немного поразмыслив мы накидали основные работы, которые надо сделать, а именно:

• Нам нужен дизайн-проект новой комнаты;
• Нам надо закупить материалы для ремонта;
• Надо составить смету ремонта;
• Надо выполнить сам ремонт;
• И т.к. мы решили сделать небольшую перепланировку, то надо согласовать ее с ТСЖ.

Отобразим эти работы в виде блоков:

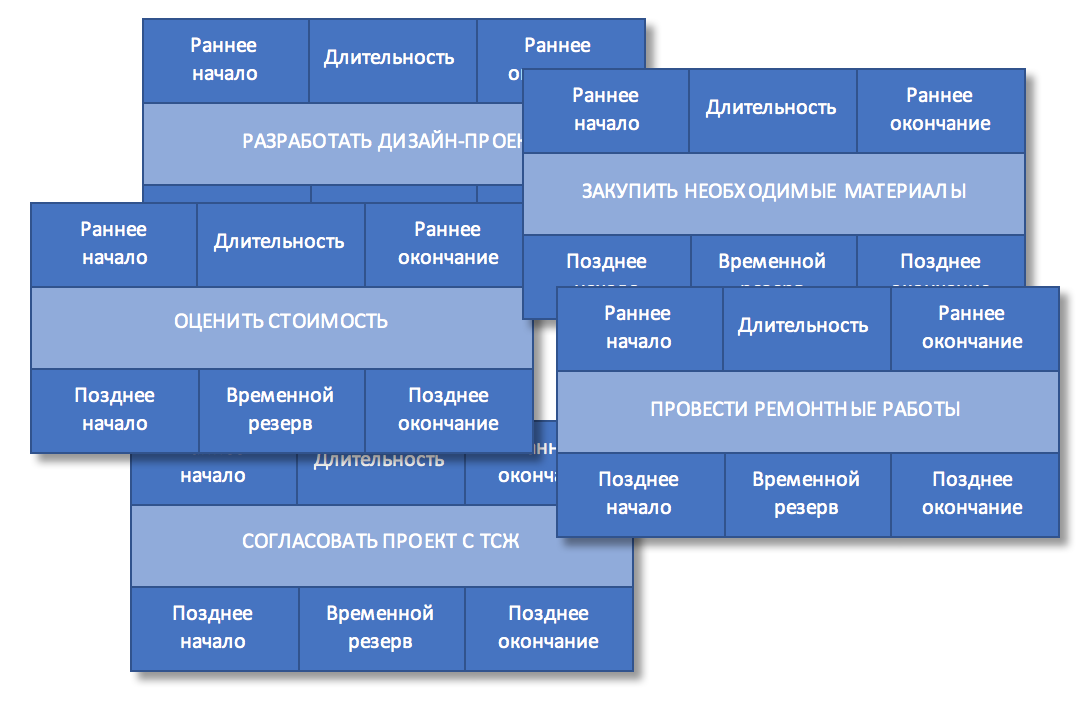
Рисунок 1. Состав работ

Шаг 4. Оценить длительность работ

Мы решили оценивать длительность работ в днях, т.к. до начала учебного года еще достаточно времени, то такая точность планирования нас вполне устраивает.

Рисунок 2. Длительность работ

Шаг 5. Определить последовательность работ

Теперь определим последовательность работ, мы будем использовать схему построения сетевого графика «сверху-вниз». Первая работа, которую необходимо выполнить — это работа «Разработать дизайн-проекта«. Затем мы оценим стоимость проекта, а параллельно начнем согласование с ТСЖ, т.к. эта задача занимает много времени. После того, как мы оценим проект и его согласуем, мы приступим к покупке всех необходимых материалов и уже затем начнем сам ремонт.

Рисунок 3. Последовательность работ

Укажем стрелками связи между работами.

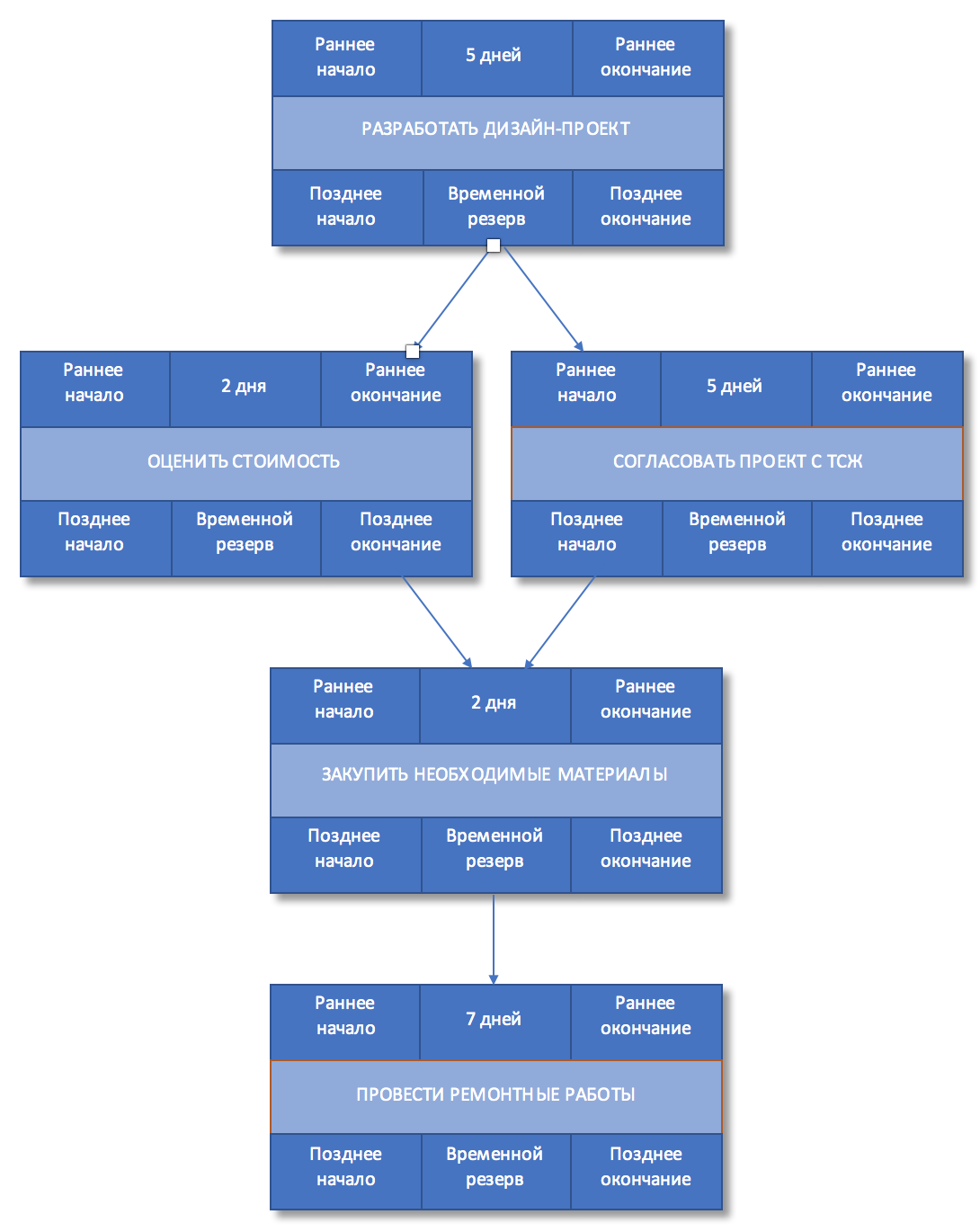
Рисунок 4. Связи между работами

Шаг 7. Определить раннее начало и раннее окончание

Т.к. мы выбрали модель сетевого график «сверху-вниз», то начинаем его и просматривать сверху вниз, начиная с самой верхней работы, и далее по очереди двигаемся к самой нижней работе.

Напомним, что раннее начало последующей работы будет совпадать с ранним завершением предшествующей, а раннее окончание каждой из работ определяется как раннее начало плюс длительность работ Если предшествующих работ несколько, то ранним началом последующей работы будет наибольшее из значений раннего окончания одной из предшествующих работ.

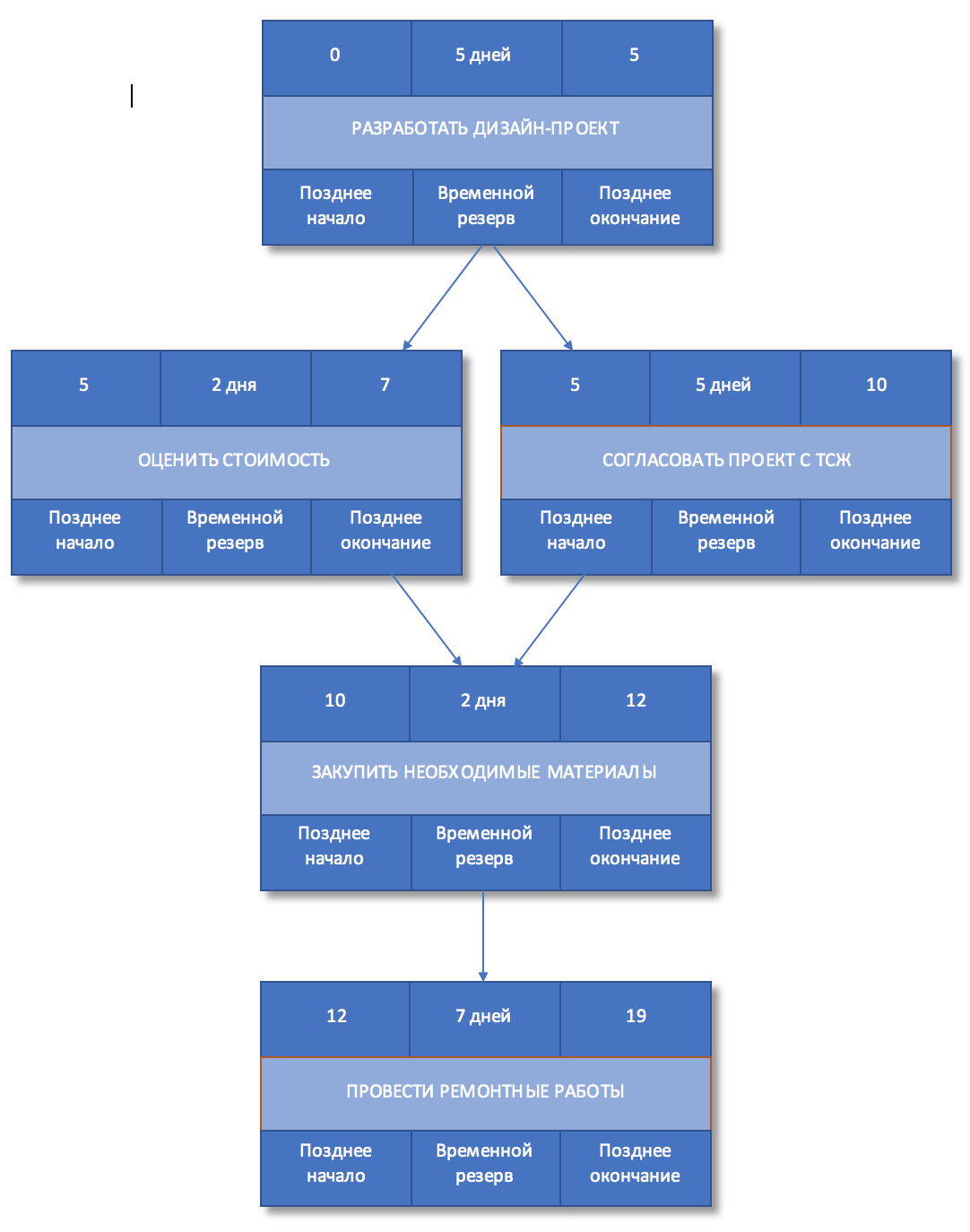
Рисунок 5. Раннее начало и окончание работ

Шаг 8. Определить поздние начало и окончание

Для того, чтобы определить поздние начало и окончание просмотрим сетевой график в обратном направлении — снизу вверх. Позднее окончание работы будет совпадать с поздним началом последующей работы. Если последующих работ несколько, то поздним окончанием работы будет наименьшее из значений позднего начала последующих работ. Позднее начало каждой работы определяется как позднее окончание минус длительность работы.

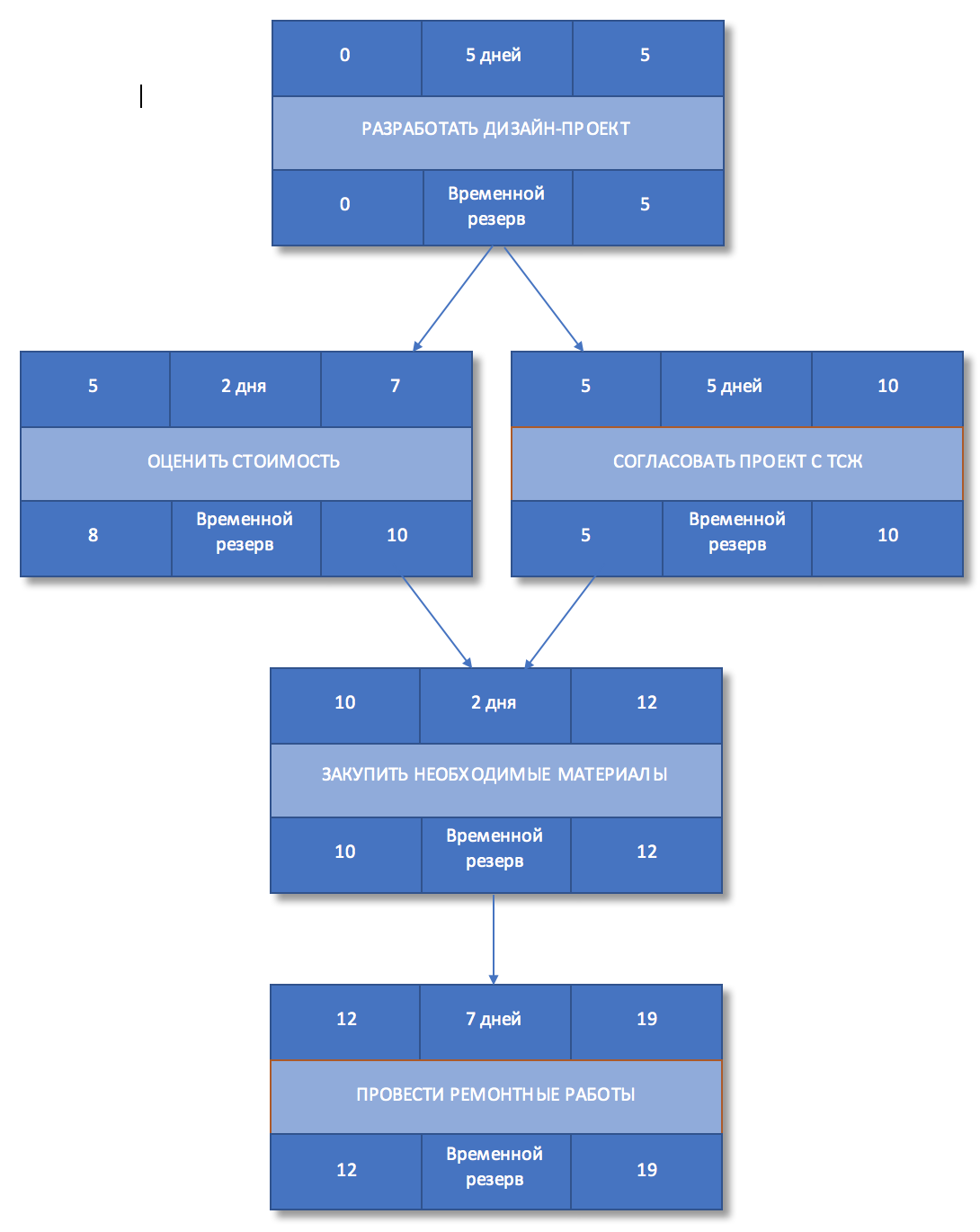
Рисунок 6. Позднее начало и окончание работ

Шаг 9. Определить временной резерв

Вычислим временной резерв для каждой из работ. Он вычисляется как разница между поздним и ранним началом или поздним и ранним окончанием работы.

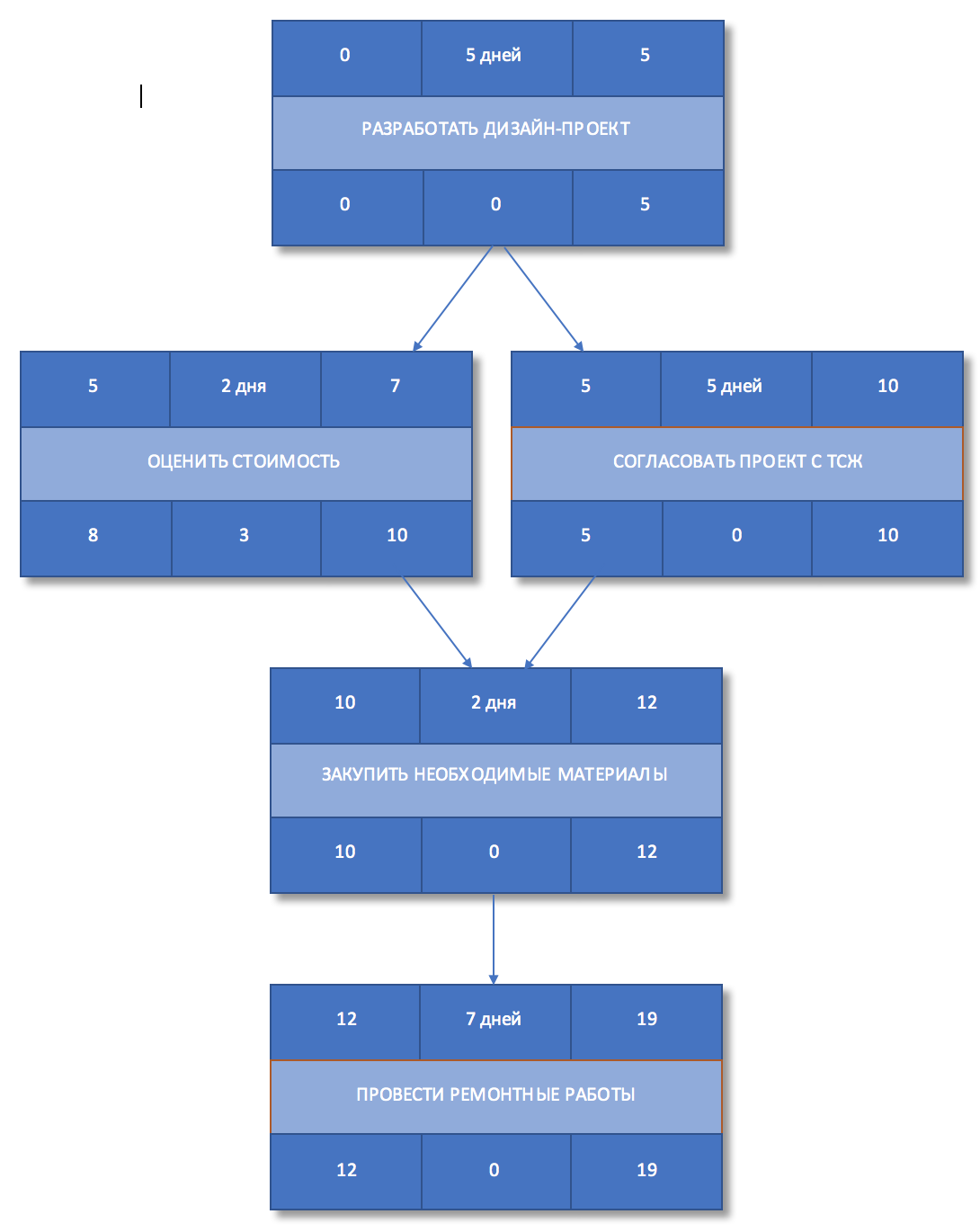
Рисунок 7. Временной резерв

Шаг 10. Выявить критический путь

Как мы уже знаем, критический путь — это цепочка работ, у которых резерв времени равен нулю. Выделим такие задачи на сетевом графике.

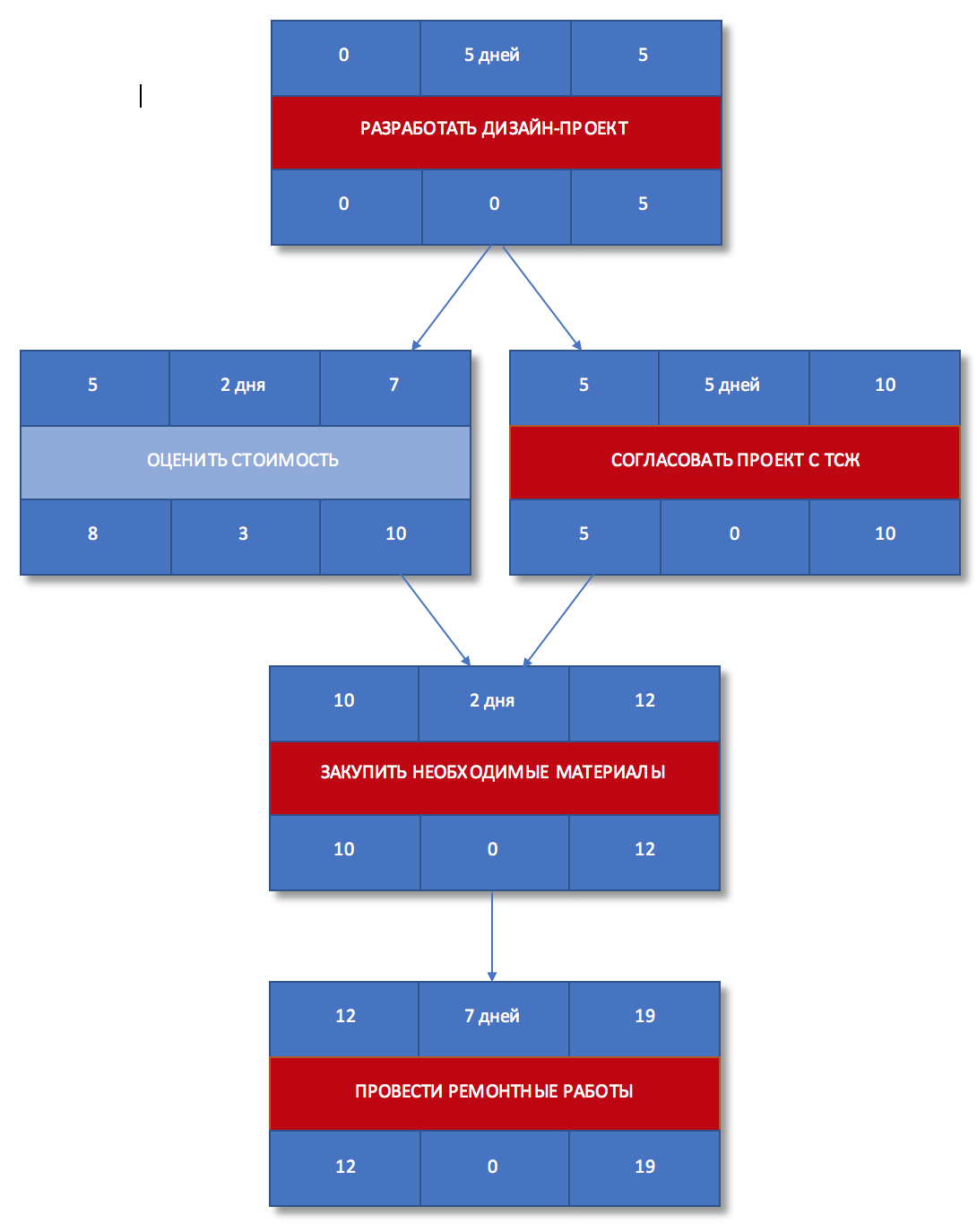
Рисунок 8. Критический путь

Задачи «Разработать дизайн-проект«, «Согласовать проект с ТСЖ» и «Закупить необходимые материалы«, «Провести ремонтные работы» составляю критический путь, а его длина составляет 19 дней. Это означает, что в текущем виде проект не может быть выполнен быстрее, чем за 19 дней. Если мы хотим сократить сроки проекта, то нам необходимо оптимизировать задачи, лежащие на критическом пути.

Например, мы можем начать ремонтные работы раньше получения согласования на перепланировку от ТСЖ, приняв на себя риски того, что согласование может быть не получено.

Просмотры:
85 703

Использование табличного метода

Общепризнанные ПП календарного планирования (MS Project, Primavera Suretrack, OpenPlan и т.п.) способны вычислять ключевые параметры сетевой модели проекта. Мы же в настоящем разделе табличным методом выполним настройку подобного расчета обычными средствами MS Excel. Для этого возьмем наш пример фрагмента проектных операций проекта в области СМР. Расположим основные параметры сетевого графика в столбах электронной таблицы.

Модель расчета параметров сетевого графика табличным способом

Преимуществом выполнения расчетов табличным способом является возможность простой автоматизации вычислений и избежание массы ошибок, связанных с человеческим фактором. Красным цветом будем выделять номера операций, располагающихся на критическом пути, а синим цветом отметим расчетные позиции частных резервов, превышающих нулевое значение. Разберем пошагово расчет параметров сетевого графика по основным позициям.

1. Ранние начала операций, следующих за текущей работой. Алгоритм расчета настраиваем на выбор максимального значения из раннего времени окончания нескольких альтернативных предыдущих действий. Взять, например, операцию под номером 13. Ей предшествуют работы 6, 7, 8. Из трех ранних окончаний (71, 76, 74 соответственно) нам нужно выбрать максимальное значение – 76 и проставить его в качестве раннего начала операции 13.
2. Критический путь. Выполняя процедуру расчета по пункту 1 алгоритма, мы доходим до конца фрагмента, найдя значение продолжительности критического пути, которая в нашем примере составила 120 дней. Значения наибольших ранних окончаний среди альтернативных действий обозначают операции, лежащие на критическом пути. Отмечаем эти операции красным цветом.
3. Поздние окончания операций, предшествующих текущей работе. Начиная с концевой работы начинаем движение в обратную сторону от действий с большими номерами к операциям с меньшими. При этом из нескольких альтернатив исходящих работ выбираем наименьшее знание позднего начала. Поздние начала вычисляем как разницу между выбранными значениями поздних окончаний и продолжительности операций.
4. Резервы операций. Вычисляем полные (общие) резервы как разницу между поздними началами и ранними началами либо между поздними окончаниями и ранними окончаниями. Значения частных (свободных) резервов получаем в результате вычитания из числа раннего начала следующей операции раннего окончания текущей.

Мы рассмотрели практические механизмы составления сетевого графика и расчета основных параметров временной продолжительности проекта. Таким образом, вплотную приблизились к исследованию возможностей анализа, проводимого с целью оптимизации сетевой модели и формирования непосредственно плана действий по улучшению ее качества. Настоящая тема занимает немного места в комплексе знаний проект-менеджера и не так уж и сложна для восприятия. Во всяком случае, каждый РМ обязан уметь воспроизводить визуализацию графика и выполнять сопутствующие расчеты на хорошем профессиональном уровне.

Методы расчета длительности операций

Для обеспечения построения, анализа и управления расписанием проекта необходимо рассчитать следующие параметры сетевого графика: стоимость, задействованные ресурсы и продолжительность работ. Требуемые ресурсы нужно рассчитать до определения продолжительности операций, так как их длительность во времени, как правило, зависит от состава задействованного ресурсного обеспечения

Кроме того, важно понимать, насколько ресурсы календарно доступны, что, в свою очередь, влияет на сроки работ и их продолжительность. Очевидно, что ключевым параметром выступает именно длительность операций

Для ее оценки используется ряд специальных методов, краткая характеристика которых приведена в табличной форме далее.

Основные методы оценки длительности операций

В случае отсутствия статистических данных по аналогичным операциям и невозможности применить экономико-математические методы расчета часто используют экспертные оценки. У данного метода есть серьезное достоинство – его простота, при условии, что удалось привлечь опытных и объективных экспертов. Но этого достичь бывает нелегко, позиции экспертов по вопросам продолжительности могут оказаться противоположными. Тем не менее, такое положение вещей вполне допустимо при использовании средневзвешенных оценок квалифицированных экспертных мнений.

В разнообразных проектах присутствуют идентичные по природе работы. Например, подготовка устава проекта, разработка ТЗ, проведение тендера по структуре и трудоемкости мало чем отличаются друг от друга. Это свойство используется для оценки длительности по аналогам. В некоторых случаях информацию о параметрах аналогичных работ вполне допустимо использовать для планирования расписания. Для этого схожесть типа и содержания операций должны быть подвергнуты экспертизе.

Параметрическая оценка длительности тесно сопряжена с нормативным подходом. Данный подход задействует такие параметры, в частности, как производительность (объем производства в единицу времени) или выработка. Например, чтобы выполнить монтаж I-го уровня сложности оборудования «А» требуется, допустим, 100 нормо-часов труда специалистов высшей квалификационной категории. Подобного рода мероприятия называют еще работами фиксированного объема, потому что продолжительность их связана с числом выделяемых ресурсов и может быть оценена как объем работ, деленный на количество человеческих ресурсов.

Помимо варианта фиксированного объема отдельно выделяется случай фиксированной продолжительности работы. Примерами таких работ являются действия, связанные с режимом дежурства на объекте, обслуживания оборудования и т.д. Продолжительность в подобных случаях обусловлена длительностью работы обслуживаемого объекта

Для параметрического метода, как мы видим, важно найти параметр, от которого зависит продолжительность операции и причинно-следственные связи, на основе которых возможно определить зависимости параметра от других значений

Построение сетевого графика

В нашем примере для построения сетевого графика необходимо составить формуляр операций, его можно использовать в качестве образца на практике.

В таблицу сведем следующие данные по каждой операции:

• номер операции;
• предшествующие операции;
• количество исполнителей;
• продолжительность операции в днях.

В таблице операций их номера соответствует нумерации в карточке-определителе в соответствии с группировкой параллельных операций.

Таблица операций для построения сетевого графика

Номер операции	Предыдущие операции	Кол-во исполнителей, чел.	Продолжительность, дни
1.	—	10	1
2.	1	2	3
3.	1	3	1
4.	1	2	4
5.	4	1	0,5
6.	3	3	2
7.	5	2	0,5
8.	2,7,6	10	0,5
9.	9	10	0,5
10.	9	1	3
11.	9	2	4
12.	9	2	2
13.	9	2	3
14.	12	2	2
15.	13	3	2
16.	10,11,14,15	10	0,5
17.	16	10	0,5
18.	17	2	2
19.	18	2	3
20.	17	2	2
21.	17	2	3
22.	21	3	1
23.	20	2	2
24.	19,22,23	10	0,5
25.	24	10	0,5
26.	25	5	1
27.	26	5	3
28.	25	3	2
29.	28	3	2
30.	25	2	4
31.	27,29,30	10	0,5
32.	31	10	0,5
33.	32	7	1
34.	32	2	1
35.	33,34	10	1

На основе таблицы операций и карточки-определителя с учетом произведенной группировки параллельных операций осуществляется построение сетевого графика.

Сетевой график, пример

Определим критический путь. Критический путь на данном сетевом графике составляют операции: 1, 4, 5, 7, 8, 9, 13, 15, 16, 17, 18, 19, 24, 25, 28, 29, 31, 32, 33 (34), 35.

В результате построения сетевого графика работы можно сделать вывод, что деятельность организации не укладывается в заданный срок равный 22 рабочим дням, составляя вместо этого 26 дней. При этом операции первой, второй и третьей недели не укладываются в заданный для них срок, равный 5 рабочим дням. По сетевой модели операции 1 недели длятся 7 дней, 2 недели – 6 дней, 3 недели – 6 дней. Операции четвертой и пятой недель укладываются в заданные для них сроки.

Для соблюдения запланированных сроков произведем корректировку сетевого графика.

В нашем примере сетевого графика по данным карточки-распределителя можно сделать вывод, что для некоторых операций в рамках запланированных действий существует резерв специалистов в отделе. Учитывая, что общая численность сотрудников относительно невелика, можно воспользоваться способом корректировки сетевой модели с привлечением дополнительных ресурсов, в качестве которых выступают свободные на момент реализации операции специалисты данного отдела. Благодаря этому сократится срок выполнения операций критического пути, соответственно и сроки всей сетевой модели. Корректировке подлежат операции 1, 2 и 3 недель, так как операции 4 и 5 недель сетевого графика укладываются в заданные сроки.

После корректировки осуществим построение альтернативного сетевого графика.

Необходимо привлечь дополнительных специалистов для выполнения операций 4 (отдел специальных программ), 13 (отдел по организации оздоровительной кампании) и 18 (отдел специальных программ). Расчет трудоемкости операций (Q) определим исходя из произведения числа специалистов (N), выполняющих операцию, на число дней (t), выделенных для ее выполнения:

Q = N * t

Q4 = 2*4 = 8 ч/дн

Q13 = 2*3 = 6 ч/дн

Q18 = 2*2 = 4 ч/дн

В отделе специальных программ работает 5 человек, но в выполнении операции 4 задействовано только 2 человека. В результате привлечения двух специалистов новый срок выполнения операции составит: 8 / 4 = 2 дня. Следовательно, операция 4 будет выполняться 2 дня вместо 4 дней.

В отделе по организации оздоровительной кампании работает 3 специалиста, но в выполнении операции 13 занято только два человека. В данном случае привлечение одного дополнительного специалиста позволит сократить срок выполнения операции: 6 / 3 = 2 дня. Следовательно, операция 13 будет выполняться 2 дня вместо 3 дней.

В выполнении операции 18 задействовано 2 специалиста отдела специальных программ. Привлечение двух дополнительных специалистов позволит сократить срок ее выполнения: 4 / 4 = 1 день. Следовательно, операция 18 будет выполняться 1 день вместо 2 дней.

В результате получаем срок выполнения операций после корректировки сетевого графика с привлечением дополнительных ресурсов:

26 – 2 – 1 – 1 = 22 дня.

Таким образом, за счет произведенной коррекции сетевого графика срок выполнения операций, соответствует изначально заданному сроку в 22 рабочих дня.

Альтернативный график будет аналогичен предыдущему в плане своей структуры, корректировке подвергнуты сроки реализации операций согласно построенной сетевой модели.

Альтернативный сетевой график

Построение сетевых графиков.

Сетевой график — это последовательная схема, отражающая порядок выполнения работ проекта. Он позволит вам провести своего рода тестирование: продумать различные стратегические подходы, прежде чем начать работы.

Сетевой график включает три элемента.

• Событие — значительное происшествие в ходе выполнения проекта; иногда также называется узловым событием или вехой. Оно не имеет протяженности во времени и не потребляет ресурсов. Это мгновенная точка отсчета в вашем проекте (как указательный столб на дороге), которая характеризует начало или конец работы или группы работ. Примеры событий: «Черновик отчета утвержден» или «Начало проектирования».

В данном случае слово «событие» употребляется в непривычном для вас контексте. В обычной жизни «событием года» мы называем, например, торжественный прием по случаю избрания нового президента. Но в отличие от нашего термина, это событие не только имеет протяженность во времени, но и требует значительных ресурсов!

• Работа — действия, которые выполняются, чтобы перейти от одного события вашего проекта к другому. Она занимает время и потребляет ресурсы. Примеры описания работ: «Разработать формат отчета» или «Сформулировать требования к новому продукту».

• Продолжительность — действительное календарное время, требуемое на выполнение работы. Также называется периодом или временем работы. Продолжительность работы зависит от ее трудоемкости, количества исполнителей (с учетом их работоспособности), производительности используемого оборудования (например, вычислительная мощность компьютера) и доступности требуемых ресурсов.

Понимание, из чего складывается это время, поможет найти средства и пути его сокращения. Предположим, для тестирования нового программного продукта нужно 24 часа. Если один работник будет заниматься этим ежедневно по шесть часов, то понадобится четыре дня. Одновременное привлечение двух исполнителей не ускорит работу, но в две смены они сделают ее за два дня.

Единицы времени применяются для описания двух взаимосвязанных, но разных характеристик работы. Продолжительность работы — это время от начала до ее завершения, в то время как трудоемкость — это количество затраченных на ее выполнение человеко-часов.

Если четыре исполнителя выполнят данную работу за пять рабочих дней, то это ее продолжительность, а трудоемкость составит 20 человеко-дней. (Трудоемкость подробнее рассматривается в главе 5.).

Чистое время задержки также включается в продолжительность работы. Например, вы отправили отчет на утверждение шефу. Он пролежал в приемной четыре дня и семь часов, после чего шеф в течение часа просмотрел и подписал отчет. Продолжительность работы в данном случае будет пять дней, хотя трудоемкость составила всего один час.

Независимо от сложности вашего проекта, его сетевой график будет содержать все те же три описанных элемента.

Алгоритм построения сетевого графика

Алгоритм построения сетевого графика по методу критического пути состоит из 10 следующих шагов.

Шаг 1. Определить основную цель проекта

Определить основную цель проекта – результат, который должен быть получен после успешного завершения проекта. Это необходимо для определения границ проекта и первоначальной оценки его сроков.

Шаг 2. Выявить ограничения

Выявить ограничения, влияющие отдельные работы проекта или весь сетевой график. Типовыми ограничениями являются доступность ресурсов, сроки или стоимость. Кроме этого, ограничения могут быть заданы законодательными требованиям.

Шаг 4. Оценить длительность работ

Оценить длительность каждой из работ и определить ресурсы, необходимые для ее успешного выполнения. Команда управления проектом должна договориться о том, какие единицы измерения использовать для оценки длительности работ (часы, дни или, например, месяцы), а также выработать требования к максимальной длительности одной работы. Все работы, превышающую эту длительность, должны быть декомпозированы.

Шаг 5. Определить последовательность работ

Определить последовательность работ. Определить работу, которая должна быть выполнена в первую очередь. В некоторых случаю таких работ может быть несколько и они будут выполняться параллельно. Эта работа должна быть самой левой на графе.

Определить работу, которая должны быть выполнена сразу же после первой. Далее определяется работа, которая должна начинаться сразу же после второй, и так далее, пока все работы не будут рассмотрены. Если работа начинается до завершения предыдущей, то предыдущую работу необходимо разделить на составляющие. Работы могут выполняться параллельно, но при условии, что связь работ точно определена.

Начало выполнения параллельных работ должно быть строго привязано к завершению предыдущих работ.

Шаг 6. Указать связи между работами

Указать связи между работами, обычно в виде стрелок, которые показывают последовательность выполнения работ. Направление стрелок устанавливается слева направо.

Шаг 7. Определить раннее начало и раннее окончание

Определить раннее начало и раннее окончание для каждой из работ. Для этого сетевой график просматривают слева направо начиная с первой работы (крайней левой) и далее по очереди двигаются к последней. Последующая работа не может быть начата до тех пор, пока не завершены все предшествующие ей работы. Раннее начало последующей работы будет совпадать с ранним завершением предшествующей.

Если предшествующих работ несколько, то ранним началом последующей работы будет наибольшее из значений раннего окончания одной из предшествующих работ. Раннее окончание каждой из работ определяется как раннее начало плюс длительность работ, оцененная на шаге 4.

Шаг 8. Определить поздние начало и окончание

Определить поздние начало и окончание для каждой из работ. Для этого сетевой график просматривают в обратном направлении — начинают с последней работы (самой правой) и далее по очереди двигаются к первой. Предшествующая работа должна быть завершена до того, как начнется каждая из последующих работ. Позднее окончание работы будет совпадать с поздним началом последующей работы. Если последующих работ несколько, то поздним окончанием работы будет наименьшее из значений позднего начала последующих работ. Позднее начало каждой работы определяется как позднее окончание минус длительность работы.

Шаг 9. Определить временной резерв

Определить временной резерв для каждой из работ. Резерв времени вычисляется как разница между поздним и ранним началом или поздним и ранним окончанием работы.

Шаг 10. Выявить критический путь

Критический путь — это цепочка работ, у которых резерв времени равен нулю. При оптимизации сетевого графика в первую очередь проводится оптимизация работ, лежащих на критическом пути.

Варианты связей и отношение предшествования

Сетевые методы планирования строятся по моделям, в которых проект представляется как целостная совокупность взаимосвязанных работ. Данные модели во многом формируются типом и видом связей между операциями реализации проекта. С позиции типа различаются жесткие, мягкие и ресурсные связи. Видовое различие взаимосвязанности операций основано на отношения предшествования. Рассмотрим основные типы связи.

Мягкие связи. Им соответствует особая, «дискреционная» логика, дающая «мягкую» основу для выбора операций к размещению на диаграмму, диктуемого технологией. В то время как технология длительный период развивалась на протяжении многих циклов, вырабатываются правила делового оборота, не требующие дополнительной фиксации и планирования. Это экономит время, место модели, стоимость и не требует дополнительного контроля со стороны PM. Поэтому менеджер проекта сам решает, нужна ему такая выделенная операция, или нет.
Жесткие связи. Данный вид связей основан на технологической логике. Они предписывают выполнение конкретных действий строго после других, что сообразно с процессуальной логикой. Например, наладку оборудования можно осуществлять только после его монтажа. Тестирование недочетов технологии допустимо проводить, если сдача ее в опытную эксплуатацию произошла и т.д

Иными словами, принятая технология (неважно, в какой сфере она реализуется) жестко навязывает последовательность мероприятий и событий проекта, что и обуславливает соответствующий тип связи.
Ресурсные связи. В условиях назначения на один ответственный ресурс нескольких задач возникает его перегруженность, что может привести к удорожанию проекта

За счет подведения под менее критичную задачу дополнительного ресурса этого можно избежать, и такие связи называются ресурсными.

В момент формирования расписания проекта сначала применяются жесткие, а затем – мягкие связи. Далее, по необходимости, некоторые мягкие связи подлежат сокращению. Благодаря этому может быть достигнуто некоторое сокращение общей длительности проекта. В условиях перегруженности некоторых ответственных ресурсов из-за параллельных работ допустимо разрешение возникших конфликтов введением ресурсных связей. Однако следует контролировать, чтобы новые связи не привели к значительным изменениям общего плана.

Сопряженные работы как некая последовательность проектной задачи связаны друг с другом. Назовем их операциями А и В. Введем понятие отношения предшествования, которое рассматривается как некое ограничение на сроки и общую продолжительность, так как операция В не может начаться до момента окончания операции А. Это означает, что В и А связаны отношением простого предшествования, при этом вовсе не обязательно, чтобы В начиналось одномоментно с окончанием А. Например, отделочные работы начинаются после возведения крыши дома, но это не означает, что выполняться они должны в тот же момент, когда наступит указанное событие.

Минимизация числа исполнителей проекта при сохранении времени его выполнения

линейная диаграммакарта проекта

• минимизировать количество одновременно занятых исполнителей;
• выровнять потребность в трудовых ресурсах на протяжении всего срока выполнения проекта.

• перемещение работ по оси времени возможно осуществлять только вправо (откладывая их начало);
• работы критического пути трогать нельзя, т. к. это приведет к увеличению срока выполнения всего проекта;
• работы, имеющие свободный резерв времени, можно спокойно перемещать на величину этого резерва;
• перемещение работ, имеющих только полный резерв времени, требует аналогичного сдвига последующих работ;
• передвигаемые работы на линейной диаграмме выделяют, отмечая заметным символом: звездочкой, штрихом, цветом и т.п.

калькулятора

Таблица 1

Работа (ij)	Длительность t(ij), дн.	Количество исполнителей
1,2	4	5
2,3	6	3
2,4	5	6
2,7	11	6
3,5	9	1
4,6	9	2
5,7	11	3
6,7	10	5
7,8	4	6

Рис. 1. Пример сетевого графика

Проведем более детальный анализ линейной диаграммы и карты проекта с целью оптимизации трудовых ресурсов: выравнивая потребность в них на протяжении всего проекта и минимизируя количество одновременно занятых исполнителей. График ежедневной потребности ресурса показывает, что минимальное число исполнителей не может быть меньше 6 человек, что определяется их потребностью для работ критического пути. А 15 исполнителей на участке 5-10 дни проекта является явно завышенным и подлежит коррекции в первую очередь.

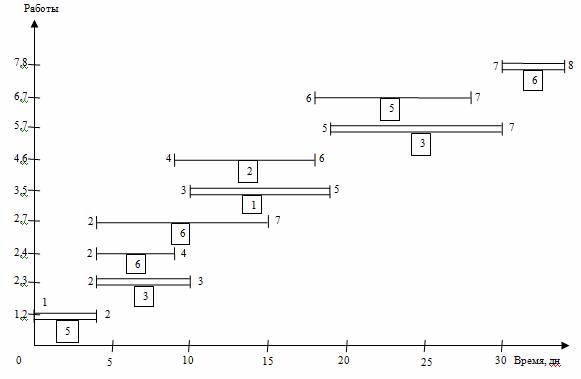
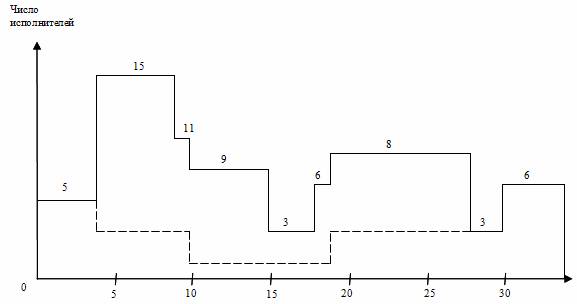Рис. 2. Линейная диаграмма и карта проекта до оптимизации

15 исполнителей заняты на работах 2,3; 2,4 и 2,7. Работу 2,3 трогать нельзя, т. к. это работа критического пути. Работа 2,4 имеет только полный резерв, но не имеет свободного резерва времени. Работа 2,7 имеет солидный свободный резерв времени и поэтому наиболее предпочтительна для оптимизации. Используем часть свободного резерва, переместив работу 2,7 (5-15 дни) на 5 дней (ее новый срок 10-20 дни). Тем самым максимально необходимое число исполнителей уменьшилось до 9 человек, т.е. задачу минимизации трудовых ресурсов проекта можно принять завершенной.

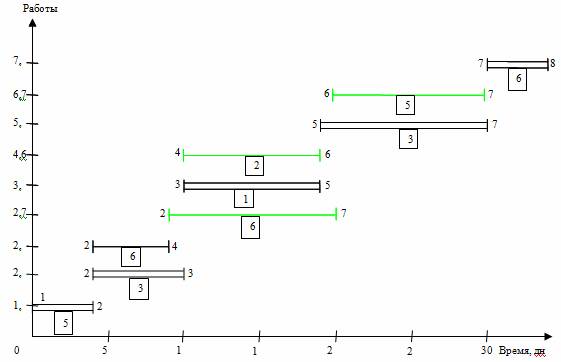
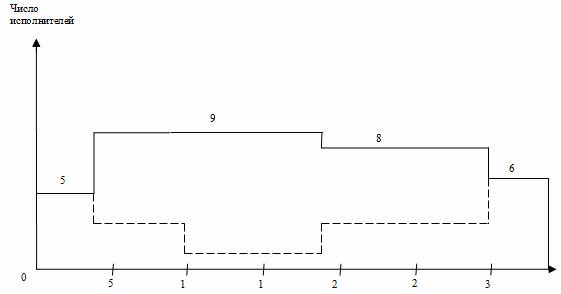
Рис. 3. Линейная диаграмма и карта проекта после оптимизации
Далее решим задачу выравнивания потребности в ресурсах, анализируя интервалы времени, связанные с «провалами» карты проекта. С учетом перемещения работы 2,7 падения спроса на исполнителей в середине проекта (16-18 дни) уже не будет, но он останется ближе к концу проекта (29-30 дни). Чтобы сгладить график загрузки, переместим работу 6,7 (19-28 дни), имеющую свободный резерв времени, на 2 дня (новый срок 21-30 дни). Также для целей выравнивания потребности в трудовых ресурсах переместим работу 4,6 (10-18 дни) на 1 день (11-19 дни).
В итоге оптимизации приходим к линейной диаграмме и карте проекта, представленными на рис. 3. Из графика видно улучшение равномерности загрузки исполнителей: новая ежедневная потребность ресурса составляет от 5 до 9 человек в зависимости от этапа выполнения проекта, резких колебаний занятости нет. Длительность выполнения всего проекта при этом осталась неизменной (34 дня), т. е. необходимое условие оптимизации соблюдено.

Видеоинструкция

Последовательность действий по моделированию

Шаг первый

Построение сетевого графика начинаем путем размещения прямоугольников задач последовательно слева-направо, применяя правила, описанные в предыдущих статьях. При выполнении моделирования методом «вершина-работа» основным элементом диаграммы выступает семисегментный прямоугольник, в составе которого отражены параметры начала, окончания, длительности, резерва времени и наименования или номера операций. Схема представления ее параметров показана далее.

Схема изображения работы на сетевом графике

Результат первого этапа построения сетевого графика

В соответствии с логикой последовательности операций с помощью специализированной программы, MS Visio или любого редактора размещаем образы работ в заданном выше формате. В первую очередь заполняем наименования выполняемых действий, их номера и длительность. Рассчитываем раннее начало и раннее окончание с учетом формулы раннего начала текущего действия в условиях нескольких входящих связей. И так проходим до завершающей фрагмент операции. При этом, в нашем примере проекта тем же графиком Ганта не предусмотрены исходящие связи от операций 11, 12, 13 и 14. «Подвешивать» их на сетевой модели недопустимо, поэтому мы добавляем фиктивные связи к конечной работе фрагмента, выделенные на рисунке синим цветом.

Шаг второй

Находим критический путь. Как известно, это путь, имеющий самую большую продолжительность действий, которые в него входят. Просматривая модель, мы выбираем связи между работами, имеющими максимальные значения раннего окончания действий. Намеченный критический путь выделяем стрелочками красного цвета. Полученный результат представлен на промежуточной схеме далее.

Схема сетевого графика с выделенным критическим путем

Шаг третий

Заполняем значения позднего окончания, позднего начала и полного резерва работ. Для выполнения расчета переходим к конечной работе и берем ее за последнюю операцию критического пути. Это означает, что поздние значения окончания и начала идентичны ранним, и от последней операции фрагмента мы начинаем двигаться в обратную сторону, заполняя нижнюю строку схематического представления действия. Модель выполнения расчета показана ниже на схеме.

Схема расчета поздних начал и окончаний вне критического пути

Итоговый вид сетевого графика

Шаг четвертый

Четвертым шагом алгоритма сетевого моделирования и расчетов выполняется вычисление резервов и коэффициента напряженности

Первым делом имеет смысл обратить внимание на полные резервы путей некритических направлений (R). Они определяются путем вычитания из продолжительности критического пути временной длительности каждого из этих путей, пронумерованных на схеме итогового сетевого графика

• R пути под номером 1 = 120 – 101 = 19;
• R пути под номером 2 = 120 – 84 = 36;
• R пути под номером 3 = 120 – 104 = 16;
• R пути под номером 4 = 120 – 115 = 5;
• R пути под номером 5 = 120 – 118 = 2;
• R пути под номером 6 = 120 – 115 = 5.